More Information
Submitted: May 27, 2024 | Approved: June 17, 2024 | Published: June 18, 2024
How to cite this article: Saeed EF. Evaluation of Performance Research Nuclear Reactors' Steady-state and Kinetic Model Analyses. Ann Civil Environ Eng. 2024; 8: 039-044.
DOI: 10.29328/journal.acee.1001064
Copyright License: © 2024 Saeed EF. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: MPM; Equations; Nuclear power; Plant kinetics
Evaluation of Performance Research Nuclear Reactors' Steady-state and Kinetic Model Analyses
Esraa Fareed Saeed*
Department of Science, Physics and Earth Sciences Curriculum Division, General Directorate of Curriculum, Ministry of Education, Iraq
*Address for Correspondence: Esraa Fareed Saeed, Department of Science, Physics and Earth Sciences Curriculum Division, General Directorate of Curriculum, Ministry of Education, Iraq, Email: [email protected]
The mainstays of nuclear substance radiation and isotopic synthesis are nuclear-powered power plants, however effective safety evaluation is made tougher by the complicated construction topologies and physical connection effects. This work proposes a multiphysics linked technique for evaluating both the kinetic and steady-state behaviors of the MPRR and LVR-15 laboratory reactors. To represent complicated member geometries, homogenized assembling sections are generated using two-dimensional whole-core computational simulations. It is discovered that the steady-state findings and the so-called Monte Carl solution comparisons correspond quite nicely. The greatest assemble power mistakes for LVR-15 and MPRR are 6.49%/10%, and the highest command rod value mistakes are 31 pcm/136 pcm, and the mistakes are 377 pcm/383 pcm, accordingly. Meanwhile, study is done on transitory procedures, such as reactivity-initiated disasters and exposed loss-of-flow mishaps. Both units' modeling findings show plausible adverse feedback events. Furthermore, it is shown that the two reactors' accident-related behaviors are comparable though having different core architecture since they employ the exact same kinds of water as a fluid. The technique to studying nuclear power plant kinetics known as Multi-Physics Simulation (MPM) is explained. Drawing on many research and verification efforts conducted at Politecnico di Milan, Italy, MPM is shown to be a valuable instrument for managing reactors security and oversight. It may be viewed as a holistic analytical tool that is implemented during the reactor architecture design phase. The capacity to concurrently answer the interrelated equations that control the many physical processes taking place in a nuclear plant inside the same simulated setting is a core characteristic of MPM.
Complex structures called nuclear power plants are made to start, regulate, and maintain nuclear reactions in chains. Although their main purpose is to produce power, they are also employed in studies, medical, and marine propulsion. Atomic fuel, usually uranium-235 or plutonium-239, is found in the center of a nuclear power plant and fissions when neutron strike it. A large quantity of power is released during the process of fission in the way of temperatures which is then utilized to create moisture, which powers turbine to produce energy.
PET kinetic models generally originate from the a single-, two-, or three-compartment model, where the input equation is a directly recorded circulating curve (concentration of radiotracer in bloodstream as a function of time). The solutions of the differential equations used in the simulation are assumed to be variables that are reflective of intrinsic kinetic attributes of the specific a tracer molecule in the system. By officially contrasting the model's output to the PET data obtained through experimentation, one can calculate values for these kinetic variables and thereby extract information about enforceable, delivery, or any conjectured process, as opposed to all other procedures that produce the material signal.
An imperfect overview of current multiphysics connection studies on human photonic crystals. In order to conduct a steady-state multi-physics connection study of the HPCR layout, the Monte Carlo (MC) code RMC, ANSYS Mechanics APDL, and a distributed simulation of elevated temperatures radiators were coupled. Thermal-mechanical input and heat conduit points of operation were examined [1]. Developed a steady-state solution relying on the RMC and the free infinite volume software Open FOAM, which to model the three-dimension (3D) thermally-mechanical operation of HPCR. This allowed for the realization of linked simulations for heat transfer, expansion of heat, and neutrons transportation. Created the multi-physics linkage based on the available open-source programs, such as OpenMC, Nektar++, and SfePy, for a kilowatt-scale project by using the functional expansion tally technique to translate information between the Monte Carlo simulation program and a finite- element simulator [2].
The development of reactors and security study depend heavily on the consideration of temporary, covering typical transient situations such as energy adaptation, nuclear starting and a break, and predicted operating events. Through the connection of a single point reactor kinetics model, a single variable core heat exchange approach, a combination heat transfer approach, an alkaline metal thermal-to-electric converters model, and a heat transfer reflector approach, the fluctuating reactions of an apparatus during initialization and disasters were modeled [3]. The radial thermal conductivity and feed pin transmission of electricity are disregarded in favor of simplification of the reactors core as a multi-layer cylinder construction with a heat conduit at its center in the aggregated variable core heat exchange model. Employed the network concept and an analogous multi-physics connection technique to mimic the thermal transfer from extreme temperatures heat pipes after they are completely operational [4].
Another of the cutting-edge energy facilities that can fulfill the objectives of the Next Generation IV Worldwide Conference (Gen-IV) is the Leader Speed Rocket (LFR) [5]. These objectives include long-term viability economics, reliability and security, diffusion opposition, and physical safeguards. Too far, this fusion reactor with fission has been the focus of multiple research and countless inquiries aimed at evaluating its possible applications.
Because of the inherent interaction between heat-hydraulics, thermal extensions, and neutrons, the Multi-Physics Modeling (MPM) method is a new instrument for analyzing the "reactor system" in this setting, both in operating and intermittent situations [6]. The MPM look at that is being suggested here involves a set of combined partially differential equations that are irregular and influenced by time. These problems must be solved concurrently in a single simulator and explain various aspects of the "physics" (such as heat exchange, fluid movement, temperature adaptability, and radiation physics) which happen in nuclear reactors [7].
The acceptance of a specific model must, in overall, be an enormous simplifying of the reality because the information provided by the PET data is insufficient to back up models with significant elegance. The analysis of parameters involves connected presumptions and constraints that must be met and reexamined on a regular basis. Occasionally, there are additionally exploratory constraints that must be taken into account [22]. The most prevalent of these limitations is the annoyance of, or explicitly advising against, getting an accurate measurement of the plasma's input its purpose. Other exploratory factors are addressed in relation to potential future medical and research uses of PET ligand studies. Lastly, we wrap up our treatment of PET kinetic modeling with a discussion of a generalized structure for executing it and further development.
Study is changing towards to how to implement the high-fidelity multi-physic connection approach as the statistical reactor idea has gained popularity in the past few years. The primary coupling phenomena in weapons is neutron-thermal interaction, and a large number of academics have conducted studies based on this topic. Linked the Computation Flow Dynamics (CFD) software STAR-CCM+ with the nuclear transfer simulation programed PENTRAN. Introduced a revolutionary fundamental multi-physics connection technique that used ANSYS/Fluent to dynamically connect the MCNP6 programed [8]. In order to connect the unit's mechanical and temperature transient assessment programs and produce more precise computation results, additional connection surfaces had been built. Presented a steady-state connected simulation technique that uses the publicly available CFD programed CFX and the Monte Carlo Analysis Code RMC to analyze a high-temperature furnace.
Yet, conventional reactor technologies like pressurized water-based reactors have received the majority of attention in prior research on multiphysics force interaction. There is currently a lack of study on multiphysics field interaction in heat transfer processors. Heating pipe neutrons are frequently engineered as solid-state nuclear power plants, employing metal alloys to provide a framework that supports the core structurally and facilitates heat transmission between the fuel sources to the temperature pipe. In addition, this highlights the importance of the neutronic-thermal-mechanical interaction phenomena within the nuclear facility [9].
By connecting the Monte Carlo algorithm RMC with the market finite elements programed, thermal stresses may surpass the highest permissible limits for the building under analysis in a 2-D heat conduit reactors design under the catastrophic disaster. According to ANSYS, just one thermal pipe collapse would cause the fuel in touch with the failing thermal pipe wall to experience markedly greater load intensity [10].
This study proposes three-dimensional multi-physics coupled analysis approach for the steady-state properties of heating pipe nuclei. To confirm the approach's correctness and practicality, a neutronic-thermal-mechanical coupled study of a representative heated pipe nuclear was conducted. Using this approach, a thorough calculation and evaluation on the selected heat transfer emitter during specified operation conditions was carried out [11]. This approach has great promise in the field of solid-state nuclear construction along with security research.
Statement of the problems
Using multiphysics models, examine the interaction consequences of several physical processes (e.g., heat hydraulics, a mechanics of structure, and neutrons) when studying nuclear power plants. Analyze study atomic reactors' steady-state operation under a variety of use scenarios, paying particular attention to variables such as rates, heat identities, and distribution of electricity [12]. Create and verify kinetic simulations to examine the temporal behavior of studies on nuclear reactors, such as reactive absorption as well as rod activity, throughout startup, a break, and operating fluctuations.
To protect the precision and dependability of the results, a thorough research approach is essential while performing a multiphysics study and analyzing experimental nuclear power plants using kinetic and steady-state models. Creating and integrating multiphysics simulation platforms that can simulate the intricate relationships among heat hydraulic systems, mechanics of structure, and neutrons inside the nuclear power system is one strategy. To examine the transient behavior of studies on nuclear power plants throughout startup, a shutdown, and operating temporary, an analytical approach to kinetic modeling is necessary [13]. This entails creating computational representations of reactor dynamics that take into account elements like control rod motion, postponed neutron predecessors, and reactive feedback processes. These models of kinetics are validated and calibrated using data collected from reactors flash testing or reference calculations.
Multi-physics illustrating strategy
The "advancing mesh" method is used to combine the formulas of solid motion with the other the sciences models to incorporate the consequences of heat expansion.
System explanation
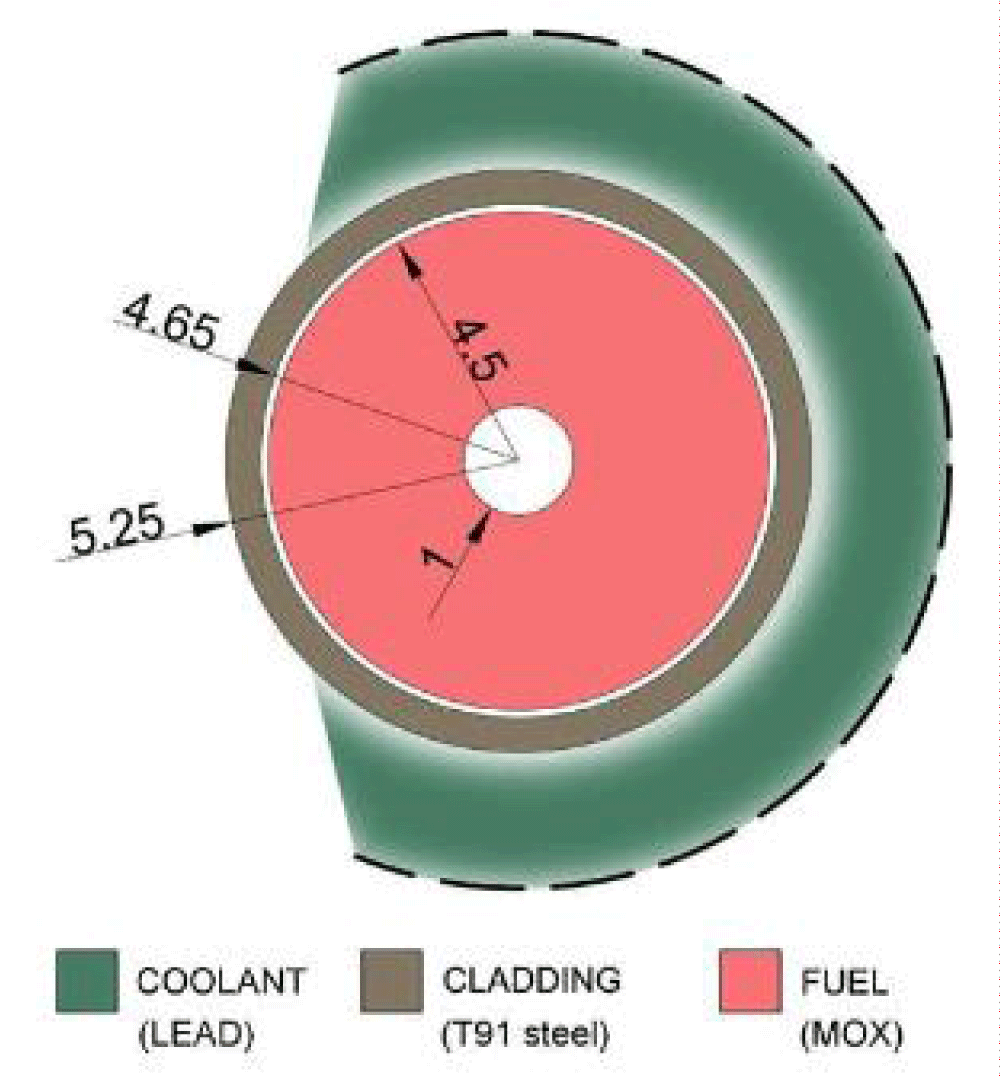
This reactor has undergone several design iterations and is currently in the process of being finalized. Its core is made up of 162 fuel gatherings, each of which has fuel screws organized in a rectangular arrangement and is encircled by reflecting device meetings [14]. In the initial meters of the dynamic elevation a passive channel that runs above the active altitude is chosen to allow for a full leader flow expansion and prevent imprecise prediction of the heat transference among the lead and the siding. It is not possible to evaluate the impact of the core radial expansion using just one-channel analysis. It is outside the purview of this work to introduce artificial remedial elements to adjust for these impacts [15] Figure 1.
Figure 1: Examined the vicinity of the lead and the fuel pin. Circumferential diameters, given in millimeters, at room temperature under normal circumstances [18].
Atomic nuclei
The neutronic version of the ELSY one-channel uses the multi-group diffusion theory to explain it. The ongoing nuclear transport solution and the balancing solutions for eight categories of antecedents are integrated across a set of six energy periods (Table 1).
| Table 1: Energy structure adopted in multi-group neutron diffusion. | ||
| Group number | Upper boundary | Lower boundary |
| 1 | 20 MeV | 2.23 MeV |
| 2 | 2.23 MeV | 0.82 MeV |
| 3 | 0.82 MeV | 67.38 keV |
| 4 | 67.38 keV | 15.03 keV |
| 5 | 15.03 keV | 0.75 keV |
| 6 | 0.75 keV | 0 keV |
Liquid mechanics and energy transfer
Liquid mechanics mainly addresses the behavior of cooling agents, which are typically fluids like water, dense water, fluid metallic substances, or gas, in the setting of nuclear power plants [24]. The following are the primary goals of researching liquid dynamics in reactors:
Phase evolution: The coolant used in reactors such as boiling water Plants (BWRs) changes from a fluid to a vapor. It is necessary to represent the physics of evaporation and boiling precisely.
Heat elimination: Making certain that the heat produced in the reactor core is effectively removed. Examining the convective heat transfer that occurs between the coolant and the fuel rods is necessary for this.
Keeping the coolant flow steady and preventing situations like flow oscillations or a divergence from boiling nucleate (DNB) are important aspects of thermal-hydraulic stability.
Heat is produced, transferred, and removed throughout the energy transfer process in the reactors. Important procedures consist of:
Heat production: The atomic fuel's disintegration process is the main source of heat production. This heat is passed from the combustibility to the coolant via the siding.
Convection: Heat is transferred through the covering substance and fuel pellet. These substances' thermal insulation affects both the pace of heat transmission and the spread of temperatures.
Radiation: Radiation transfer of heat can also be important in high temperatures reactors, particularly in those that are gas-cooled or fluid metal-cooled.
Heat transport, dynamics of fluids, and neutron kinetics are all analyzed in a metaphysics investigation into nuclear reactors. The primary objective is to develop a thorough model that depicts the interplay among these many physical occurrences. This includes:
Nuclear flux and distribution of power have an impact on the rates at which heat is generated in the reactor core. Nuclear kinetics and thermal-hydraulic interaction. On the other hand, the reactor's level of reactivity is impacted by the coolant's density and temperatures, which also affect neutrons moderating and absorbing properties [25].
Steady-state analysis: The reactor's operation is examined under continuous conditions of operation in steady-state models. To guarantee the reactor runs effectively and safely, heat identities, fluid rate calculations, and neutrons flux dispersion are computed.
Kinetic analysis: The changing reaction of the reactor to modifications in conditions of operation is the main focus of kinetic models. Studying transitory occurrences such as reactor beginning, a shutdown, or unintentional reactive inserts falls under this category. The simulations take temperature variations, fluid motion, and neutrons flux dependent on time behavior into consideration.
Vibrating texture and strong mechanics
The Maximum Pressure model incorporates the subsequent linear stretching equations in order to adjust for the impacts of combustion and covering temperature growth:
~ −2u−t2 = ∇ · {(17) {= 1 2 [(∇u) + (∇u)T ] (18) { = C : ({ − ˛th (T − Tref)
To make the answer to the issue simpler, the rate of thermal contraction, the value of the Young modulus, and the Dispersion factor are all held constant with respect to warmth. According to the isotropic substance theory, the rigidity matrix C may be derived using the Poisson ratio and the youngest elasticity [15]. Fuel particle columns are modeled as a single, uninterrupted structure. Irradiation-induced fracturing along with additional mechanical phenomena (such creep) is isregarded. When contrasted to the time-scales of the changes discussed in this study, the movement of these consequences may generally be thought of as sluggish [16] Figure 2.
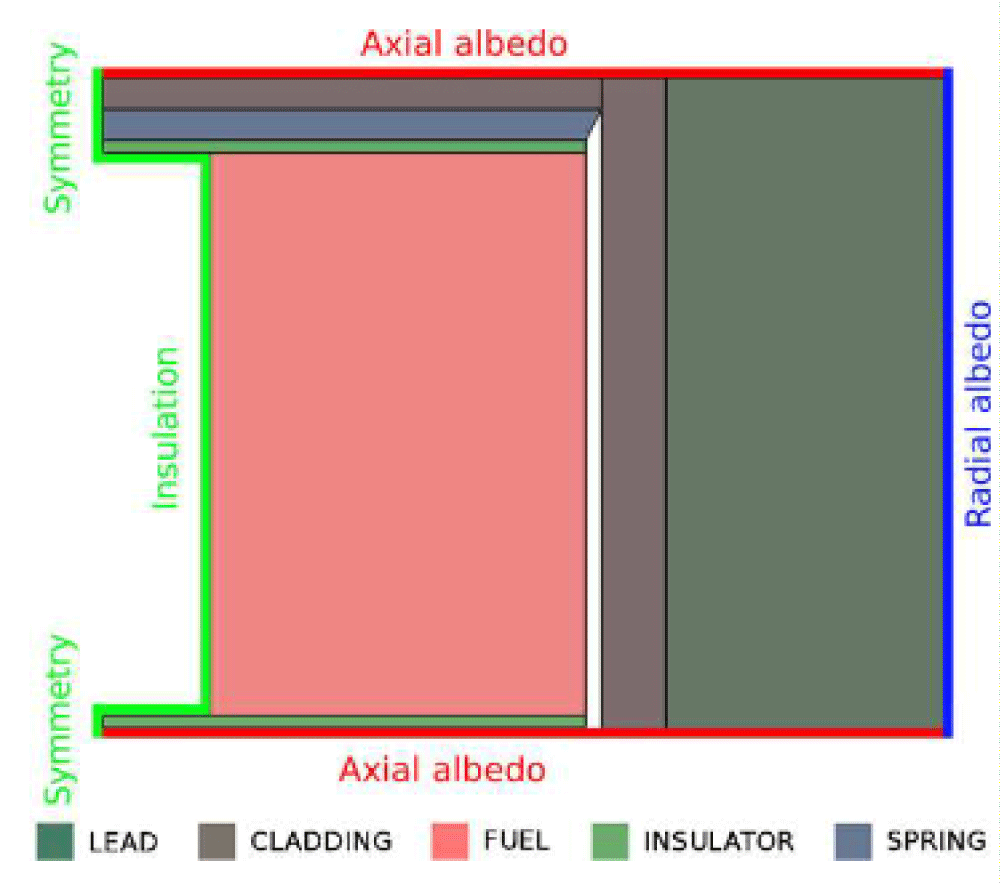
Figure 2: Main boundary conditions applied for the neutron model [18].
In fluctuations, there is a substantial difference between the two areas as a result of the radial growth of the covering and propellant. As a result, the networks of border vertices that are facing one another over the gap continuously alter. The thermal radiation model has computation challenges as a result of these phenomena [17]. Border delineation is carried out among each node of the covering interior and the fuel's exterior node in order to address this problem. In this manner, any node in the fuel outside border engages with the nearest cluster in the siding inner barrier at every time increment.
This work, which focuses on the intrinsic calculation of the coupled effects involving the thermal expansion, is not equipped to evaluate such events. To replicate the mechanical characteristics of a spring, the spring situated between the plug and the top thermal insulator can be effectively represented as an unbreakable cylinder with an appropriately adjusted Young modulus. To make things simpler, the gravitational pull is disregarded.
The COMSOL "moving mesh" methodology, also known as the arbitrary Lagrangian–Eulerian method, enables a mesh of the modeled domain to be dynamically deformed. In the current study, the shape of the model is redefined at each solution iteration using thermal-mechanical distortions. In this sense, the shifting field of the fuels and the covering affect the various physics.
Therefore, the linked effects of thermal expansion—such as the lowering of gap resistance to heat and fuel growth feedbacks on electronics—are taken into explicit account. Due to axial growth of the gasoline and the siding, the two fields go through high relative dis- placement during fluctuations. As a result, the mesh border nodes that are facing one another across the gap continuously alter. The radioactive heat transfer model has computing challenges as a result of these phenomena. A boundary mapping is carried out between the nodes of the cladding inner surface and the fuel outer surface nodes in order to address this problem. In this manner, every node in the fuel outer border engages with the nearest node in the covering inner barrier at every time step.
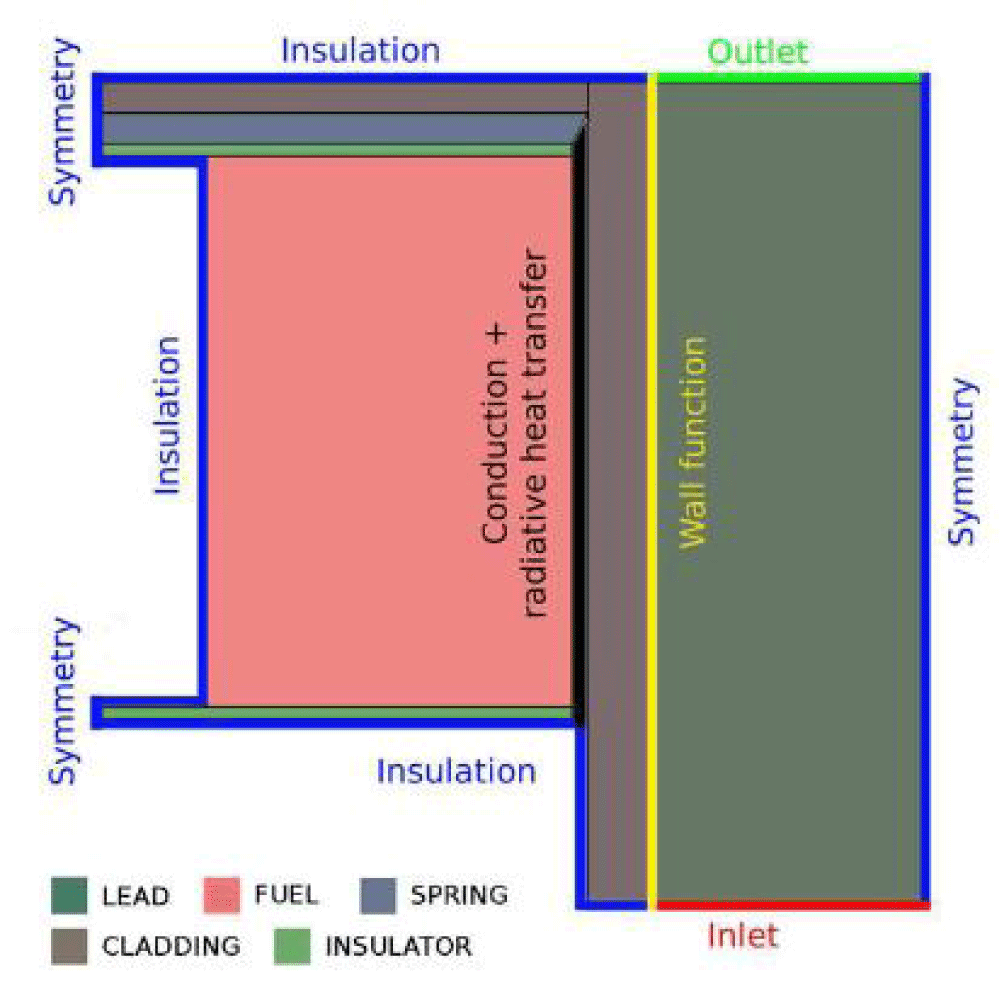
The primary parameters used for the nuclear model are summarized in Figure 3. The current concept is restricted to a just one core stream. The selection of the neutronic limits is therefore a significant question. It is determined that the reflectance boundary values provide a reasonable trade-off between computing demands and the precision of the geographic characterization of neutron emissions [18]. The COMSOL simulation area is subject to albedo limitations at its the upper, lower, and tangential bounds, specifically:
n · (D∇‑g ) = − z - g
n · (D∇‑g ) = − r - g
The primary parameters used for the thermal-fluid dynamic framework are summarized in Figure 3. Both the top border of the steel stopper and the bottom edge of the upper mechanical isolator are subject to a thermally insulated requirement [19].
Figure 3: Principal Boundary circumstances for the changing thermal-fluid model are used [18].
In order to accommodate for the vicinity channel, symmetry criteria are taken into consideration at the fluid domain's outer diameter. The lead's inlet temperature and velocity are set at the lower border. To enable the examination of fluctuations such as a loss of circulation or a decrease of heat sink, time dependence can be applied to these parameters [20]. To facilitate appropriate flow growth below its active elevation the design has a 30-cm-long dormant entry channel. The point of outlet pressures (pout) and the absence of viscosity stress are placed as outlet conditions for boundaries at the upper border of the fluid region. The conventional wall function is used to address the boundary issue at the contact between molten lead and sheathing.
Regarding the solid mechanical model, the bottom borders of the sheathing region and the lower thermally insulators are subject to an axial movement constraint. The wire mesh cannot be displaced radially at the channels outside diameter [21].
The shifting mesh higher border is compelled to conform to the axial expansion and contraction of the coating inside the lead region.
Monte Carlo solutions and simulation results
For a given object form, we apply a Monte Carlo simulation approach identical to the one used to calculate the average excluded volume. An object of the desired form is positioned such that its center lines up with the center of an L-shaped box. The volume of the box is selected to be more than the excluded volume, but still small enough to reduce the quantity of trials that are wasted. The object's orientation is determined by the three Euler angles, which are: 0 ≤ φ ≤ 2π, 0 ≤ θ ≤ π, and 0 ≤ φ ≤ 2π. A random beginning orientation is supplied to the item. The first and last Euler angles are selected from a uniform random distribution, while the second Euler angle is obtained from a random distribution to provide random isotropic orientations [26].
Our simulation outcomes for hVexi for a pair of the same rectangular prisms are shown in Table 2 along with the logically obtained hVexi for different aspect ratios of the prisms. The simulation results are inconsistent with the anticipated analytic numbers, for example, the simulation output surpasses the analytical result for squares by 3.92%. We observe that the variation in percentage raises when the length of one side grows smaller than the other two, and reduces as the length of a single side becomes much bigger than the other two (i.e., as the prism approaches a width less stick). Additionally, models for soft core rectangular spheres have also been conducted.
| Table 2: Simulation outcomes for hVexi for a pair of the same rectangular prisms. | ||||
| Aspect Ratio | Monte Carlo | Calculated | Absolute Difference | Percentage Difference |
| Platelets | ||||
| 0.000001 | 1751600.0 ± 467.911 | 2000002.000 | 248402.0 | 12.420% |
| 0.01 | 182.760 ± 0.048 | 207.02 | 24.260 | 11.718% |
| 0.5 | 11.488 ± 0.002 | 12.000 | 0.513 | 4.272% |
| 0.6 | 11.058 ± 0.002 | 11.533 | 0.475 | 4.118% |
| 0.7 | 10.804 ± 0.001 | 11.257 | 0.453 | 4.027% |
| 0.8 | 10.659 ± 0.001 | 11.100 | 0.441 | 3.975% |
| 0.9 | 10.591 ± 0.001 | 11.022 | 0.431 | 3.911% |
| Cube | ||||
| 1 | 10.569 ± 0.001 | 11.0 | 0.431 | 3.918% |
| Prisms | ||||
| 2 | 11.543 ± 0.003 | 12.0 | 0.477 | 3.811% |
| 4 | 15.023 ± 0.003 | 15.500 | 0.477 | 3.077% |
| 8 | 22.774 ± 0.007 | 23.250 | 0.476 | 2.047% |
| 16 | 38.654 ± 0.016 | 39.1250 | 0.471 | 1.204% |
| 32 | 70.624 ± 0.046 | 39.12500 | 0.439 | 0.617% |
| 64 | 134.599 ± 0.175 | 135.03125 | 0.432 | 0.320% |
Table 2 Our simulation outcomes for hVexi for a pair of the same rectangular prisms are shown in Table 2 along with the logically obtained hVexi for different aspect ratios of the prisms. The simulation results are inconsistent with the anticipated analytic numbers, for example, the simulation output surpasses the analytical result for squares by 3.92%. We observe that the variation in percentage raises when the length of one side grows smaller than the other two, and reduces as the length of a single side becomes much bigger than the other two (i.e., as the prism approaches a width less stick). Additionally, models for soft core rectangular spheres have also been conducted.
However, it is generally acknowledged that the fundamental kinematic formula is accurate, and the literature on the topic indicates that the expression needs to hold for all convex bodies. Moreover, it appears that no assumptions on the smoothness of the bodies under consideration are made in the derivations of the fundamental kinematic formula [27-31].
Our Monte-Carlo results show an interesting departure from the mathematically expected values, and given the wide-ranging implications of the excluded volume idea, the subject deserves more investigation.
The ELSY reactor's only-channel performance is being studied using the suggested MP model in both steady-state and two temporal situations: a reactive insert and a modified intake lead heat temporal. The consequences of expansion due to heat have been considered and disregarded in brief assessments. With respect to quantitative integration, the multi-physics model technique demonstrated good results by enabling simultaneous evaluation of a large number of core variables (such as heat field, movement field, and neutrons flux), their locations, and their temporal development. Due to the link between the neutronic, thermal-elastic, and fluid-dynamic processes, the temperature-driven suggestions on responsiveness (i.e., Doppler Effect, fuel axial, and coolant expansions) are directly estimated. As anticipated, fuel's longitudinal contraction has a considerable impact on the LFR behavior while being lower than the Doppler Effect.
- Nguyen N, Nguyen K, Huynh T, Vo D, Tran H. Conceptual design of a 10 MW multipurpose research reactor using VVR-KN fuel. Sci Technol Nucl Install. 2020;2020:1-10.
- Almachi JC, Sánchez-Espinoza VH, Imke U. High-Fidelity Steady-State and Transient Simulations of an MTR Research Reactor Using Serpent2/Subchanflow. Energies. 2022; 15(4):1554.
- Ferraro D, García M, Valtavirta V, Imke U, Tuominen R, Leppänen J, et al. Serpent/SUBCHANFLOW pin-by-pin coupled transient calculations for the SPERT-IIIE hot full power tests. Ann Nucl Energy. 2020; 142:107387.
- Zhang T, Li Z. Variational nodal methods for neutron transport: 40 years in review. Nucl Eng Technol. 2022;59(9):3181-3204.
- Khan DA, Khan N, Ilyas N, Gul MT. Mechanisms of Stress Tolerance in Halophytic Plants. The Metascience. 2024;2(2):9-16.
- Ibrar M, Rahim K, Ullah S, Gul MT. A Brief Overview On The Highly Medicinal Plant Genus Gomphrena. The Metascience. 2024;2(1):84-91.
- Khan N, Ilyas N, Gul MT. Mycorrhizal Associations' Significance for Plant Nutrition. The Metascience. 2024;2(2):1-8.
- Ullah I, Khan N, Gul MT. Plants' Physiological Reactions to Climate Change. The Metascience. 2024;2(1):76-83.
- Xiao W, Sun Q, Liu X, He H, He D, Pan Q, Zhang T. Application of stiffness confinement method within variational nodal method for solving time-dependent neutron transport equation. Comput Phys Commun. 2022;108450.
- Sun Q, Zhang T, Liu X, Chai X, Xiong J. A Discrete-Ordinates Variational Nodal Method for Solving Multidimensional Neutron Transport Equation with Unstructured Mesh. In: International Conference on Nuclear Engineering. American Society of Mechanical Engineers; 2022. pp. ICONE29–91525.
- Zhang T, Xiao W, Yin H, Sun Q, Liu X. VITAS: A multi-purpose simulation code for the solution of neutron transport problems based on variational nodal methods. Ann Nucl Energy. 2022;178:109335.
- Tang J, Huang M, Zhao Y, Maqsood S, Ouyang X. Numerical investigations on the melting process of the nuclear fuel rod in RIAs and LOCAs. Int J Heat Mass Transfer. 2018;124:990-1002.
- Wang J, Wang Q, Ding M. Review on neutronic/thermal-hydraulic coupling simulation methods for nuclear reactor analysis. Ann Nucl Energy. 2020;137:107165.
- Dambrosio A, Ruˇsˇc´ak M, Mazzini G, Musa A. Neutronic analysis of the LVR-15 research reactor using the PARCS code. Ann Nucl Energy. 2018;117:145-154.
- Phan G, Tran HN, Nguyen KC, Tran VP, Hoang VK, Ha PNV, et al. Comparative analysis of the Dalat nuclear research reactor with HEU fuel using SRAC and MCNP5. Sci Technol Nucl Install. 2017;2017:.
- Arinkin FM, Shaimerdenov AA, Gizatulin S, Dyusambaev DS, Koltochnik SN, Chakrov PV, et al. Core conversion of VVR-K research reactors. At Energy. 2017;123(1):17-24.
- Evans JA, DeHart MD, Weaver KD, Keiser DD. Burnable absorbers in nuclear reactors – a review. Nucl Eng Des. 2022;391:111726.
- Feng K, Wu Y, Hu J, Jin X, Gu H. Preliminary analysis of a zirconium hydride moderated megawatt heat pipe reactor. Nucl Eng Des. 2022;388:111622.
- Guo H, Buiron L, Sciora P, Kooyman T. Optimization of reactivity control in a small modular sodium-cooled fast reactor. Nucl Eng Technol. 2020;52:1367-1379.
- Guo H, Feng KY, Gu HY, Yao X, Bo L. Neutronic modeling of megawatt-class heat pipe reactors. Ann Nucl Energy. 2021;154:108140.
- Im J, Jeong MJ, Choi N, Kim KM, Cho HK, Joo HG. Multiphysics analysis system for heat pipe cooled micro reactors employing PRAGMA-OpenFOAM-ANLHTP. Nucl Sci Eng. 2023;197:1743-1757. doi:10.1080/00295639.2022.2143209
- Li J, Cai J, Li X. Conceptual design and feasibility analysis of a megawatt level low enriched uranium heat pipe cooled reactor core. Ann Nucl Energy. 2023;181:109576. doi:10.1016/j.anucene.2022.109576
- Liu L, Liu B, Xiao Y, Gu H, Guo H. Preliminary thermal and mechanical analysis on the reactor core of a new heat pipe cooled reactor applied in the underwater environment. Prog Nucl Energy. 2022;150:104306. doi:10.1016/j.pnucene.2022.104306
- Liu X, Zhang R, Liang Y, Tang S, Wang C, Tian W, et al. Core thermal-hydraulic evaluation of a heat pipe cooled nuclear reactor. Ann Nucl Energy. 2020;142:107412. doi:10.1016/j.anucene.2020.107412
- Ma Y, Chen E, Yu H, Zhong R, Deng J, Chai X, et al. Heat pipe failure accident analysis in megawatt heat pipe cooled reactor. Ann Nucl Energy. 2020;149:107755. doi:10.1016/j.anucene.2020.107755
- Morris ED, Endres CJ, Schmidt KC, Christian BT, Muzic Jr. RF, Fisher RE. Kinetic modeling in positron emission tomography. 2004;539.
- Aufiero M, Cammi A, Fiorina C, Luzzi L, Sartori A. Development of advanced simulation tools for circulating-fuel nuclear reactors. 2014.
- Zhang T, Yang M, Luo C. Multi-physics coupled analyzes of research nuclear reactors based on steady-state and kinetics models. Ann Nucl Energy. 2022;196:110231.
- He H, Chai X, Liu X. Multi-physics coupled analyzes of research nuclear reactors based on steady-state and kinetics models. Ann Nucl Energy. 2022;196:110231.
- Baker DR, Sreenivasan S. Discrepancy between Monte-Carlo results and analytic values for the average excluded volume of rectangular prisms. 2002.
- Eugene H. Discrepancy between Monte-Carlo results and analytic values for the average excluded volume of rectangular prisms. 2002.